树
树是一种分层的抽象模型。现实生活中最常见的树的例子就是家谱,或是公司的组织架构图,如下图所示: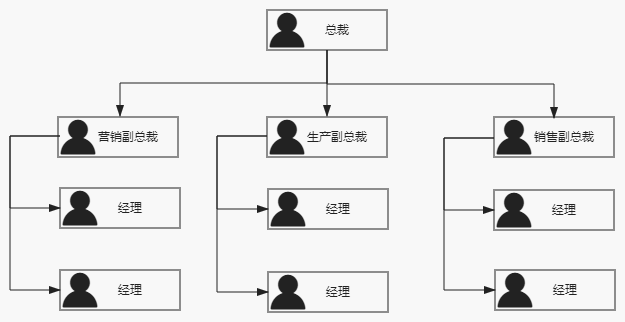
树的相关术语
一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点(除了顶层的第一个节点)以及零个或多个子节点。
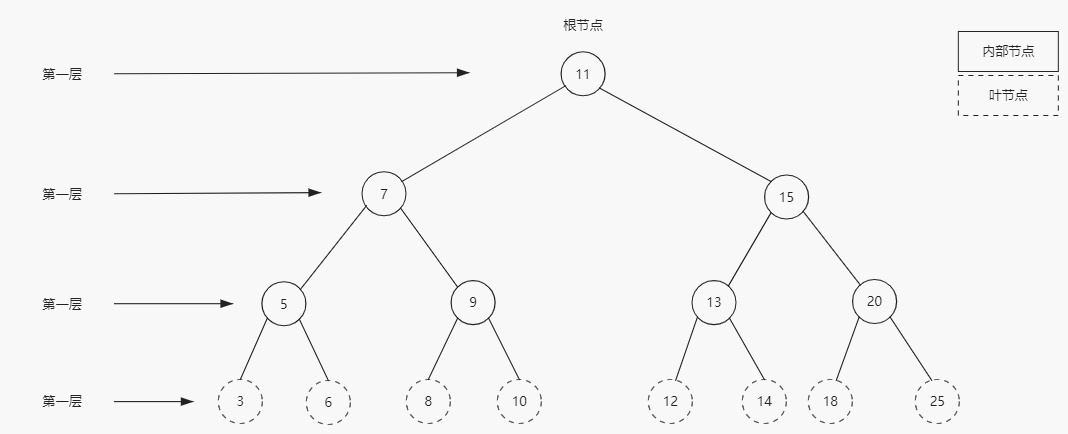
位于树顶部的节点叫作根节点。它没有父节点。树种的每个元素叫做节点,节点分为内部节点和外部节点。至少有一个子节点的节点称为内部节点。没有子元素的节点称为外部节点或叶节点
一个节点可以有祖先和后代,一个节点(除了根节点)的祖先包括父节点、祖父节点等。一个节点的后代包括子节点、孙节点等
有关树的另一个术语是子树。子树由节点和它的后代构成。
节点的一个属性是深度,节点的深度取决于它的祖先节点数量。
树的高度取决于所有节点深度的最大值。
二叉树和二叉搜索树
二叉树种的节点最多只能有两个子节点:一个是左侧子节点。另一个是右侧子节点。这个定义有助于我们写出更搞笑地在树种插入、查找、删除节点的算法。
二叉搜索树(BST)是二叉树的一种,但是只允许你在左侧节点存储(比父节点)小的值,在右侧节点存储(比父节点)大的值。
8.1.1 创建BinarySearchTree类
我们先来创建Node类来表示二叉搜索树种的每个节点,代码如下:
1
2
3
4
5
6
7
| class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
|
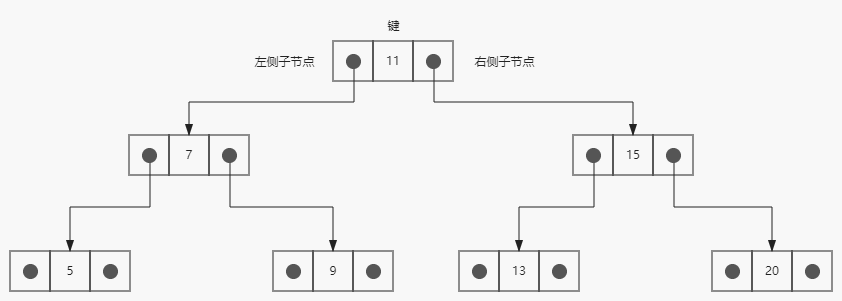
下图展现了二叉搜索树数据结构的组织方式。
 !
!
和链表一样,我们将通过指针来表示节点之间的关系。在双向链表中,每个节点包含两个指针,一个指向下一个节点,一个指向上一个节点。对于树,使用同样的方式(也使用两个指针),但是一个指向左侧节点,一个指向右侧节点。
下面我们来声明BinarySearchTree类的基本结构
1
2
3
4
5
| export default class BinarySearchTree {
constructor() {
this.root = null;
}
}
|
然后我们需要实现一些方法:
insert(value):向树中插入一个新的键。
search(value):在树中查找一个键。如果节点存在,则返回true;如果不存在,则返回false。
inOrderTraverse():通过中序遍历方式,遍历所有节点。
preOrderTraverse():通过先序遍历方式,遍历所有节点。
postOrderTraverse():通过后序遍历方式,遍历所有节点。
min():返回树中最小的值。
max():返回树中最大的值。
remove(value):从树中移除某个键
8.1.2 向二叉搜索树中插入一个键
我们先来写插入方法的主体方法:
1
2
3
4
5
6
7
8
9
| insert(value) {
if (this.root == null) {
this.root = new Node(value);
} else {
this.insertNode(this.root, value)
}
}
|
我们来写一下递归用到的辅助方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| insertNode(node, value) {
if (value < node.value) {
if (node.left == null) {
node.left = new Node(value);
} else {
this.insertNode(node.left, value);
}
} else {
if (node.right == null) {
node.right = new Node(value);
} else {
this.insertNode(node.right, value);
}
}
}
|
我们来尝试用一下insert()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| let bst = new BinarySearchTree();
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
|
上面就会创建如图所示的树结构:
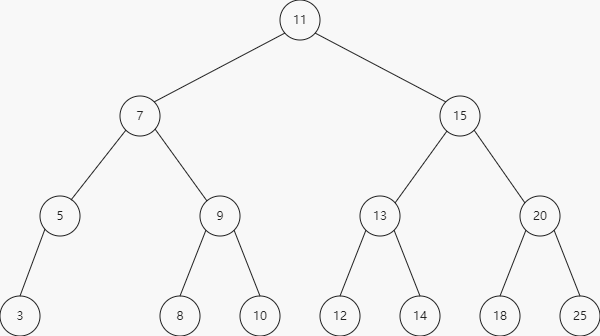
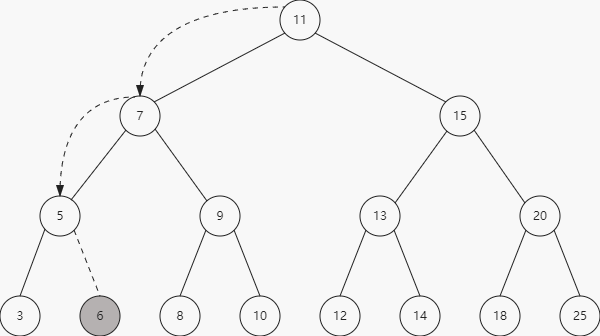
同时我们想要插入一个值为6的,执行以下代码:
运行示意图如下:
8.2 树的遍历
遍历一棵树是指访问树的每个节点对他们进行某种操作的过程。但是我们应该怎么去做呢?应该从树的顶端还是低端开始呢?从左开始还是右开始呢?访问树的所有节点有三种方式:中序、先序和后序
8.2.1 中序遍历
中序遍历是一种以上行顺序访问BST所有节点的遍历方式,也就是从最小到最大的顺序访问所有节点。中序遍历的一种应用就是对数进行排序操作。
我们先来写主方法:
1
2
3
| inOrderTraverse(callback) {
this.inOrderTraverseNode(this.root, callback)
}
|
inOrderTraverse方法接收一个回调函数作为参数。回调函数用来定义我们对遍历到每个节点进行的操作(这也叫做访问者模式)。由于我们需要用到递归用到的辅助方法,下面来写:
1
2
3
4
5
6
7
| inOrderTraverseNode(node, callback) {
if (node != null) {
this.inOrderTraverseNode(node.left, callback);
callback(node.value);
this.inOrderTraverseNode(node.right, callback)
}
}
|
我们来用一下上面的方法:
1
| bst.inOrderTraverse((value) => console.log(value))
|
下面的结果会在控制台上输出(每个数将会输出在不同的行上)
3 5 6 7 8 9 10 11 12 13 14 15 18 20 25
下图绘制了inOrderTraverse方法的访问路径。
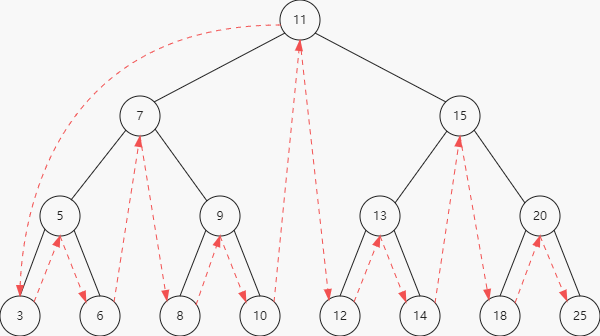
8.2.2 先序遍历
先序遍历是以优先于后代节点的顺序访问每个节点的。先序遍历的一种应用是打印一个结构化的文档:
下面我们来看实现:
1
2
3
4
5
6
7
8
9
10
11
| preOrderTraverse(callback) {
this.preOrderTraverseNode(this.root, callback);
}
preOrderTraverseNode(node, callback) {
if (node != null) {
callback(node.value);
this.preOrderTraverseNode(node.left, callback);
this.preOrderTraverseNode(node.right, callback);
}
}
|
下面描绘了preOrderTraverse方法的路径:
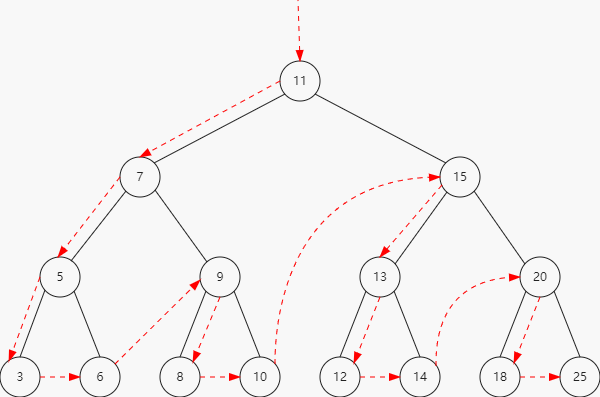
8.2.3 后序遍历
后序遍历则是先访问节点的后代节点,再访问节点本身。后序遍历的一种应用是计算一个目录及其子目录中所有文件占用空间的大小。
我们来看实现:
1
2
3
4
5
6
7
8
9
10
11
| postOrderTraverse(callback) {
this.postOrderTraverseNode(this.root, callback);
}
postOrderTraverseNode(node, callback) {
if (node != null) {
this.preOrderTraverseNode(node.left, callback);
this.preOrderTraverseNode(node.right, callback);
callback(node.value);
}
}
|
下图描绘了postOrderTraverse方法的访问路径:
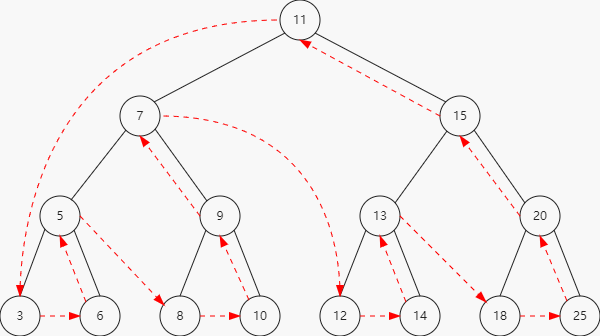
8.3 搜索树中的值
在树中,有三种经常用到的搜索类型:
我们依次来看:
8.3.1 搜索最小值和最大值
我们使用下面的树作为示例:
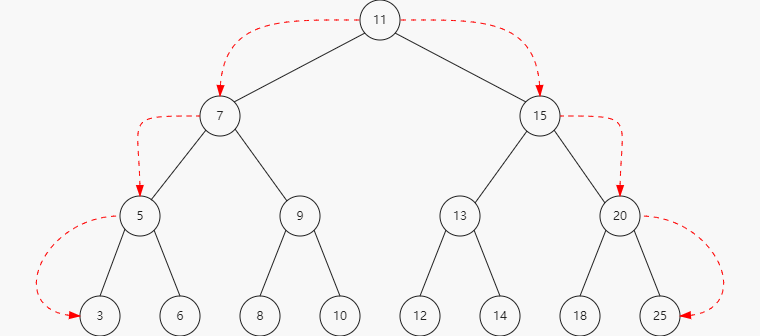
只用眼睛看这张图,你能立刻找到两个最小值和最大值吗?
如果你看一眼树最后一层最左的节点,会发现它的值为3,这是树中最小的值。如果你再看一眼最右端的节点,会发现它的值是25,是这颗树的最大值。
所以我们来实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
min() {
return this.minNode(this.root);
}
minNode(node) {
let current = node;
while (current != null && current.left != null) {
current = current.left;
}
return current;
}
max() {
return this.maxNode(this.root);
}
maxNode(node) {
let current = node;
while (current != null && current.right != null) {
current = current.right;
}
return current;
}
|
8.3.2 搜索特定的值
我们依旧用递归的方式去寻找值这个跟插入有些类似:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| search(value) {
return this.searchNode(this.root, value);
}
searchNode(node, value) {
if (node == null) {
return false;
}
if (value < node.value) {
return this.searchNode(node.left, value);
} else if (node.value > value) {
return this.searchNode(node.right, value);
} else {
return true;
}
}
|
我们可以用过以下代码来测试这个方法:
1
2
| console.log(bst.search(1) ? '找到1' : '找不到1');
console.log(bst.search(8) ? '找到8' : '找不到8');
|
输出结果如下:
8.4 移除一个节点
我们来为二叉搜索树来实现最后一个方法,也就是remove。这个方法比较复杂我们来慢慢解析
我们通过画图来比较直观的呈现过程:
1、移除一个叶节点
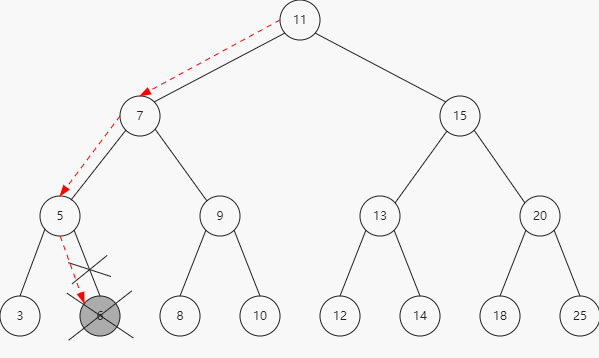
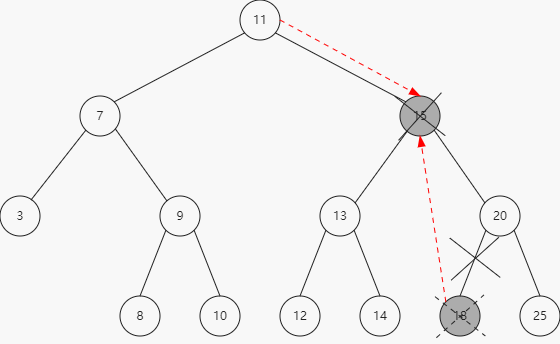
2、移除有一个左侧或右侧子节点的节点
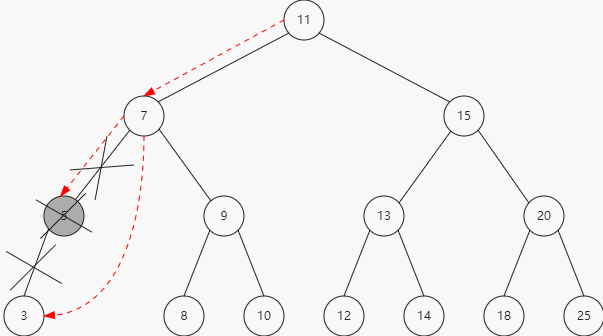
3、移除有两个子节点的节点
接下来我们用代码实现:主方法:
1
2
3
| remove(value) {
this.root = this.removeNode(this.root, value);
}
|
我们再来看看递归辅助方法的实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| removeNode(node, value) {
if (node == null) {
return null;
}
if (value < node.value) {
node.left = this.removeNode(node.left, value);
return node;
} else if (value > node.value) {
node.right = this.removeNode(node.right, value);
return node;
} else {
if (node.left == null && node.right == null) {
node = null;
return node;
}
if (node.left == null) {
node = node.right;
return node;
} else if (node.right == null) {
node = node.left;
return node;
}
const aux = this.minNode(node.right);
node.kty = aux.value;
node.right = this.removeNode(node.right, aux.value);
return node;
}
}
|


 !
!