8.4 自平衡树

BST树会存在一个问题：取决于你添加的节点数，树的一条边可能会非常深；也就是说树的一条分支会有很多层，而其它却有几层，如下图所示

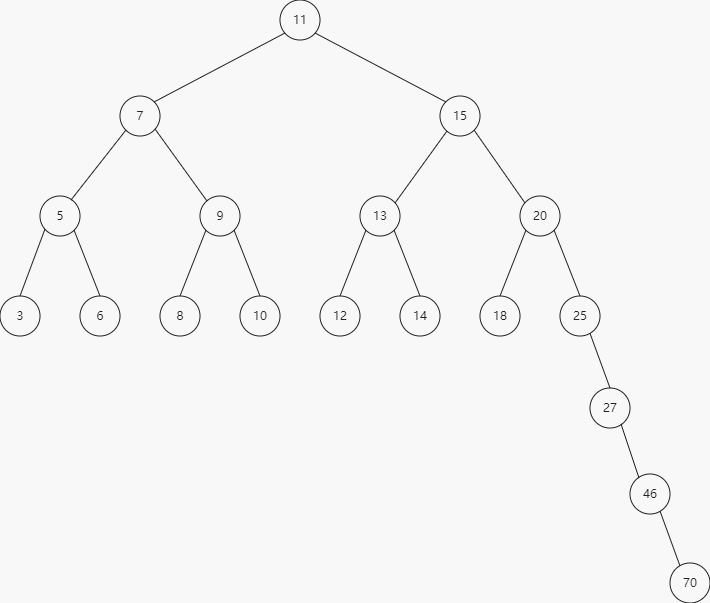
BST树深度差异.png

这会在需要的某条边上添加、移除和搜索某个节点时引起一些性能问题。为了解决这个问题，我们需要去平衡它的高度。

8.4.1 自平衡树-AVL树

AVL树是一种自平衡树。添加或移除节点时，AVL树会尝试保持自平衡，任意一个节点（不论深度）的左子树和右子树高度最多相差1.添加或移除节点时,AVL树会尽可能尝试转换为完全树。

我们开始创建AVLTree类：

1
2
3
4
5
6
export default class AVLTree extends BinarySearchTree {
    constructor() {
        super();
        this.root = null;
    }
}

AVL树也是一个BST，我们继承BinarySearchTree类，只需要重写insert、insertNode和removeNode方法。

在AVL树中插入或移除节点和BST完全相同。然而，AVL树的不同之处在于我们需要检验它的平衡因子，如果需要，会将其逻辑应用于树的自平衡。

1. 节点的高度和平衡因子

我们知道，节点的高度是从节点到其任意子节点的边的最大值。如图所示：

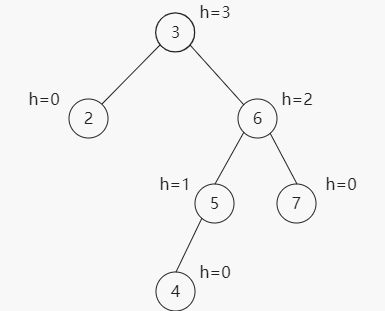
节点高度.png

所以我们需要一个计算节点高度的方法：

1
2
3
4
5
6
getNodeDeep(node) {
    if (node == null) {
        return -1;
    }
    return Math.max(this.getNodeDeep(node.left), this.getNodeDeep(node.right)) + 1;
}

结点的平衡因子 = 左子树的高度 - 右子树的高度

插入和删除操作都会导致AVL树的自我调整（自我平衡），使得所有结点的平衡因子保持为+1、-1或0。

当子树的根结点的平衡因子为+1时，它是左倾斜的（left-heavy)。

当子树的根结点的平衡因子为 -1时，它是右倾斜的(right-heavy)。

一颗子树的根结点的平衡因子就代表该子树的平衡性。

计算一个节点的平衡因子方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const BalanceFactor = {
    UNBALANCED_RIGHT: 1,
    SLIGHTLY_UNBALANCED_RIGHT: 2,
    BALANCED: 3,
    SLIGHTLY_UNBALANCED_LEFT: 4,
    UNBALANCED_LEFT: 5
}
getBalanceFactor(node) {
    const heightDifference = this.getNodeDeep(node.left) - this.getNodeDeep(node.right); //左子树的高度 - 右子树的高度
    switch (heightDifference) {
        case -2:
            return BalanceFactor.UNBALANCED_RIGHT;
        case -1:
            return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;
        case 1:
            return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;
        case 2:
            return BalanceFactor.UNBALANCED_LEFT;
        default:
            return BalanceFactor.BALANCED;
    }
}

保持所有子树几乎都处于平衡状态，AVL树在总体上就能够基本保持平衡。

2.平衡操作-AVL旋转

在对AVL树进行添加或移除节点后，我们要计算节点的高度平验证树是否需要旋转。分为四种场景：

  • 左-左（LL）：向右的单旋转
  • 右右（RR）：向左的单旋转
  • 左-右（LR）：向右的双旋转（先LL旋转，再RR旋转）
  • 右-左（RL）：向左的双旋转（先RR旋转，再LL旋转）
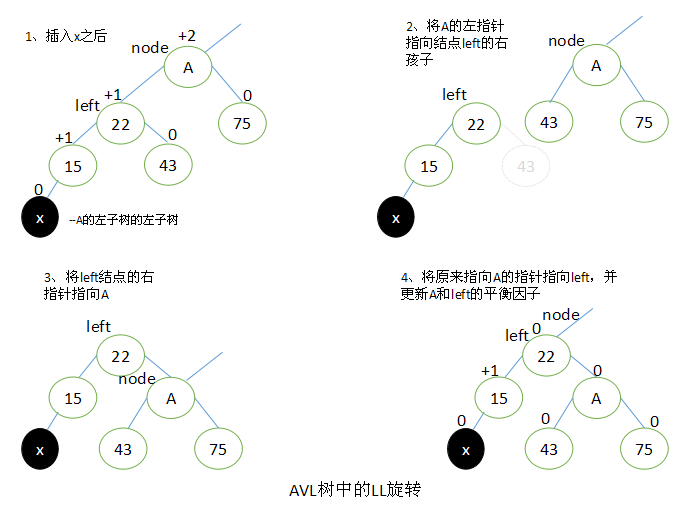
2.1 左-左（LL）：向右的单旋转

如下图所示，当x位于A的左子树的左子树上时，执行LL旋转。

设left为A的左子树，要执行LL旋转，将A的左指针指向left的右子结点，left的右指针指向A，将原来指向A的指针指向left。

旋转过后，将A和left的平衡因子都改为0。所有其他结点的平衡因子没有发生变化。

平衡树LL旋转.png

下面代码举例说明了整个过程：

1
2
3
4
5
6
rotationLL(node) {
    const tmp = node.left;
    node.left = tmp.right;
    tmp.right = node;
    return tmp;
}
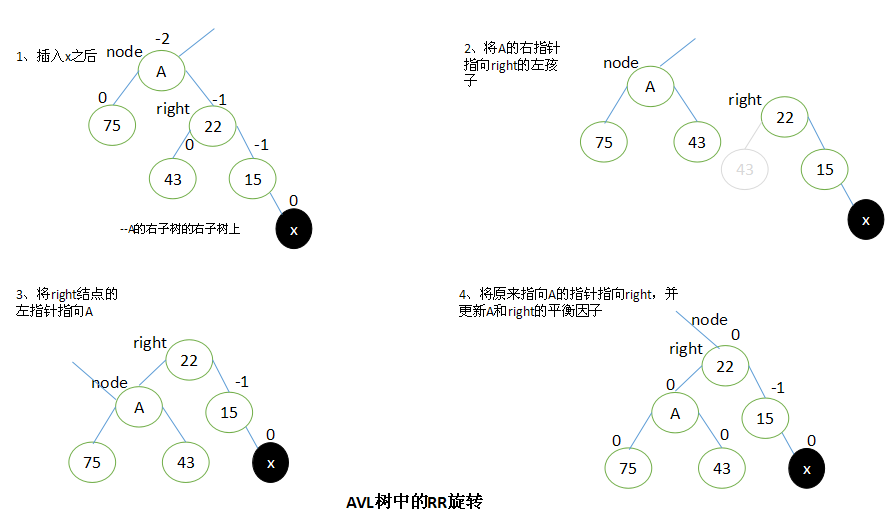
2.2 右右（RR）：向左的单旋转

当x位于A的左子树的右子树上时，执行RR旋转。

RR旋转与LL旋转是对称的关系。

设A的右子结点为Right。要执行RR旋转，将A的右指针指向right的左子结点，right的左指针指向A，原来指向A的指针修改为指向right。

完成旋转以后，将A和left的平衡因子都修改为0。所有其他结点的平衡因子都没有改变。

平衡树RR旋转.png

下面代码列举了整个过程：

1
2
3
4
5
6
rotationRR(node) {
    const tmp = node.right;
    node.right = tmp.left;
    tmp.left = node;
    return tmp;
}
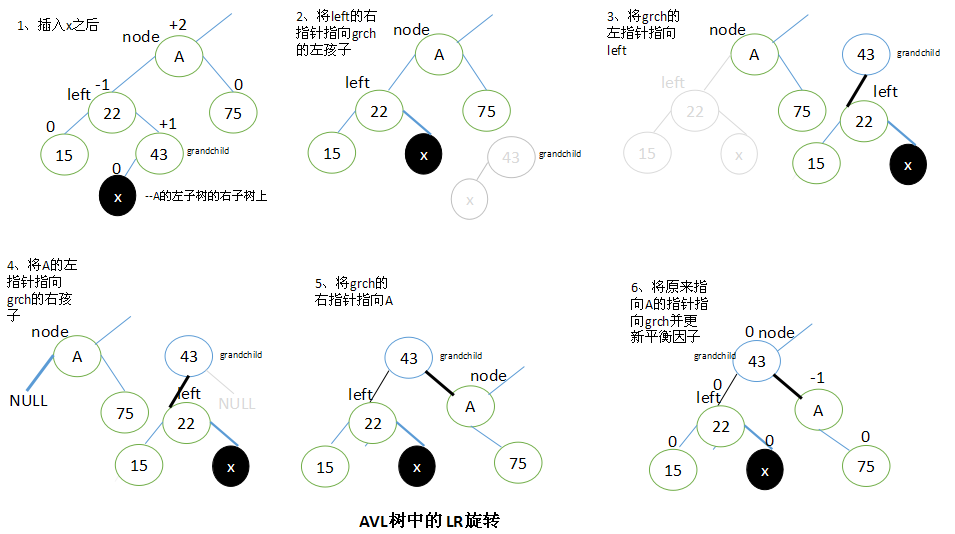
2.3 左-右（LR）：向右的双旋转（先LL旋转，再RR旋转）

当x位于A的左子树的右子树上时，执行LR旋转。

设left是A的左子结点，并设A的子孙结点grandchild为left的右子结点。

要执行LR旋转，将left的右子结点指向grandchild的左子结点，grandchild的左子结点指向left，A的左子结点指向grandchild的右子结点，再将grandchild的右子结点指向A，最后将原来指向A的指针指向grandchild。

执行LR旋转之后，调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子值。

如果grandchild结点的原始平衡因子为+1，就将A的平衡因子设为-1，将left的平衡因子设为0。

如果grandchild结点的原始平衡因子为0，就将A和left的平衡因子都设置为0。

如果grandchild结点的原始平衡因子为-1，就将A的平衡因子设置为0，将left的平衡因子设置为+1。

在所有的情况下，grandchild的新平衡因子都是0。所有其他结点的平衡因子都没有改变。

平衡树LR旋转.png

下面代码说明了整个过程：

1
2
3
4
rotationLR(node) {
    node.left = this.rotationRR(node.left);
    return this.rotationLL(node);
}
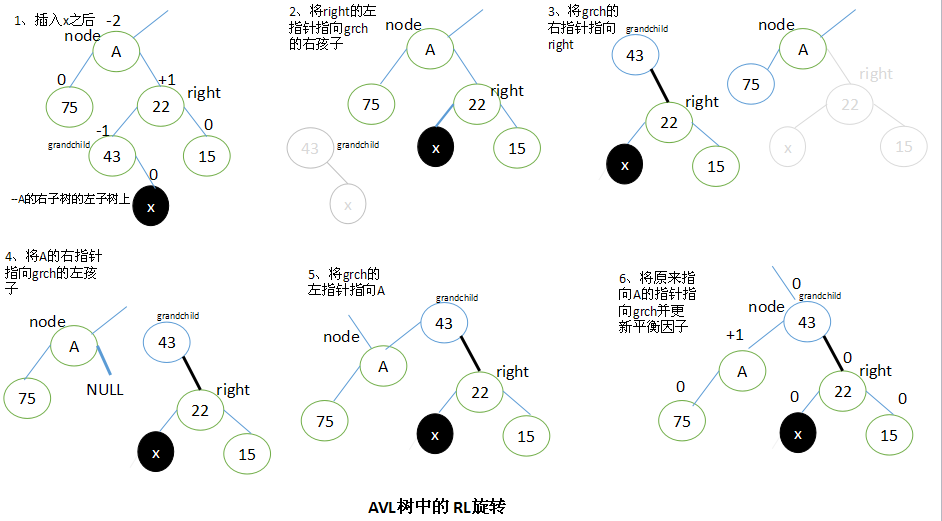
2.4 右-左（RL）：向左的双旋转（先RR旋转，再LL旋转）

当x位于A的右子树的左子树上时，执行RL旋转。

RL旋转与LR旋转是对称的关系。

设A的右子结点为right，right的左子结点为grandchild。要执行RL旋转，将right结点的左子结点指向grandchild的右子结点，将grandchild的右子结点指向right，将A的右子结点指向grandchild的左子结点，将grandchild的左子结点指向A，最后将原来指向A的指针指向grandchild。

执行RL旋转以后，调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子。这里也有三种情况需要考虑：

如果grandchild的原始平衡因子值为+1，将A的平衡因子更新为0，right的更新为-1；

如果grandchild的原始平衡因子值为 0，将A和right的平衡因子都更新为0；

如果grandchild的原始平衡因子值为-1，将A的平衡因子更新为+1，right的更新为0；

在所有情况中，都将grandchild的新平衡因子设置为0。所有其他结点的平衡因子不发生改变。

平衡树RL旋转.png

下面代码说明了整个过程：

1
2
3
4
rotationRL(node) {
    node.right = this.rotationLL(node.right);
    return this.rotationRR(node);
}
3. 向AVL树插入节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
insert(value) {
    this.root = this.insertNode(this.root, value);
}

insertNode(node, value) {
    if (node == null) {
        return new Node(value)
    } else if (value < node.value) {
        node.left = this.insertNode(node.left, value);
    } else if (value > node.value) {
        node.right = this.insertNode(node.right, value);
    } else {
        return node; //重复的键
    }
    //如果需要，将树进行平衡操作
    let balanceFactor = this.getBalanceFactor(node);
    if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
        if (value < node.left.value) {
            node = this.rotationLL(node);
        } else {
            node = this.rotationLR(node);
        }
    }
    if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
        if (value > node.right.value) {
            node = this.rotationRR(node);
        } else {
            node = this.rotationRL(node);
        }
    }
    return node;
}
4. 从AVL树移除节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
removeNode(node, value) {
    node = super.removeNode(node, value);
    if (node == null) {
        return node; //不需要进行平衡
    }
    // 检查树是否平衡
    const balanceFactor = this.getBalanceFactor(node);
    if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
        if (
            this.getBalanceFactor(node.left) === BalanceFactor.BALANCED ||
            this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT
        ) {
            return this.rotationLL(node);
        }
        if (this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {
            return this.rotationLR(node.left);
        }
    }
    if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
        if (
            this.getBalanceFactor(node.right) === BalanceFactor.BALANCED ||
            this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT
        ) {
            return this.rotationRR(node);
        }
        if (this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {
            return this.rotationRL(node.right);
        }
    }
    return node;
}